Students realize that school education is limited. But this limit dates from the 1960s. It is therefore necessary to redesign the school programs, to go to the useful and the daily.
Our school programs are refunded each year. Often they are simplified. Other times, finance adds information. The added information is often impossible to apply on everyday life. Moreover, according to the book Leading Mind by Howard Gardner, even if the best schools make the best use of the mix and the practice, it is necessary to admit that the teachers do not check if the pupil will be able to use a theory towards a convenient.
Also the students’ lessons are very esoteric and specialized, whereas it is possible to explain very complex theories with understanding the current life.
Mathematics lessons will every have the same approach: theory’s statement then theory’s demonstration. The student will participate most often with the exercises. Only ambitious or docile students will seem motivated by this forbidding order.
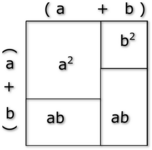
Before, students were trying to use geometry to demonstrate algebra. You see in this article a demonstration of a remarkable identity, by geometry. Thus, with such a demonstration, it is possible that the entire classroom demonstrates, by itself, a remarkable identity. In 2012, a socialist deputy, whom could take over geometry at the heart of school programs, spends time to tell.
These complex directions have a purpose. Only students initiated with the school’s interest will be motivated. That is not told to primary. There is indeed a lot of work to tell the school’s foundations and the main subjects.
Also, poor students are largely unmotivated with the fact that graduates can not find an attractive job, knowing that 80% of hires are coopted. It is indeed difficult for a poor student, lower recognized, to be admitted for that he really knows to do.
These boring and poorly explained lessons are also meant to become emotional, so we think with the short view, so we do not know how to change society. Indeed accounting studies teach you, besides with professors whom did not practice, that it is enough to have working capital for a company to go well. In fact, you have to know each business sector.
To go further, the curves and the zones representing linear equations or inequations induce that the world can be understood in two dimensions, or that certain problems can not be solved.
This does not brainstorm imagination. Now we know that there is the choice to understand more easily the infinite and our economy, with logarithmic spirals, below. These spirals can easily make sense of demographic change over time, thanks to science.
An explanation of this logarithmic spiral is in the Larouche-Riemann method. You may find it in some economics books. As you can see, this spiral uses 3 dimensions. This allows to better understand some economy‘s parameters, based on demography, with the cone, the energy’s making on the inner curve. The example above is the evolution of a ideal world’s growth for a republican society.
Sources
My Notes
Try to solve the doubling of the square, without using measurements.
